老年退役选手的复建之路
-
P220. 存在重复元素 III
题不难,滑动窗口+区间求个数,但是我直接写了个map套树状数组的两个log的做法被卡常了,重新写一遍离散化

这三个方法返回的都是指针,所以要减去首地址
lower_bound返回的是第一个>=该元素的指针
upper_bound返回的是第一个>该元素的指针
注意一下临界的细节就行
P2290. 到达角落需要移除障碍物的最小数目
01最短路,没啥好说的
倒是稀疏矩阵怎么建图还需要想想
P2897. 对数组执行操作使平方和最大
按位贪心

P2876. 有向图访问计数
正着做很难,把边全部反向就会发现是一个环套树的森林,可以转换为每一个节点能够由多少个节点达到,如果树中没有环这个值就是节点的深度。
那么我们将大环看成根,缩点之后就很好做了。首先找该连通分量中的环,先通过判重获得环中一个顶点,然后再沿着该顶点一路将环中所有点找到,初始化它们的答案值,最后跑一遍dfs就行了。
细节还是蛮多的
LCP 20. 快速公交
妈的这题卡了半天
首先考虑到玩家坐公交车的数量一定比较少且当较远路程的时候大部分时间一定花在坐车上,所以想当然的建图跑最短路
写到一半之后发现这是个假算法,在顶点为1e6以上的时候仍然可以存在步行部分路程,所以这题只能贪心
那么显然从终点倒推是最优的,注意到一个事实就是为了坐一班车,假设该车可跳跃的倍数为jump[i],那么步行的距离一定不会超过jump[i],否则一定绕了远路。所以就模仿Dijkstra的过程,从终点到起点进行稀疏图的最短路就好了。因为前面的结论,实际上该图的有效顶点和有效边数量相当少。

-
P85. 最大矩形
单调栈裸题,导下标导了半天

-
P629. K 个逆序对数组
一眼二维dp,只要算每一位对答案的整体贡献(准确的说是这一位对排在它后面元素的贡献)就可以,容易发现选择一位之后它不会影响后面选择的任何答案
dp[i][j]代表确定好前i位,逆序对数量为k的方案数
直接打了个暴力裸上去了本地跑最大测试点1.5s然后一提交超时...
注意到转移的时候本质上就是区间加,所以维护前缀数组就好,复杂度严格O(n^2)
P1751. 最多可以参加的会议数目 II
很逆天的一题
首先这个模型是线段模型,是比01背包更简单的,因为选择某条线段的之后只会影响和它有交集的线段;更具体地说,选择某条线段之后剩余选择的线段只能从左端点严格大于其右端点的线段中找
那么显然把所有线段按照左端点排序,但是线段长度规模是1e9,我就一开始打了离散化+排序,dp[i][j]代表从x坐标i开始选择,已经选择j条线段的最大代价
然后就超时了...2e6的数据规模愣是支持不了sort+两次lower_bound就只能重新修改做法,仍然是把线段按照左端点排序,dp[i][j]代表第0~i-1条线段都不能选,已经选择j条线段的最大代价
那么转移的时候需要找到选择该线段之后恰好能选择的下一条编号最小的线段,可以用upper_bound快速查找
时间是1e6的一个sort+一次upper_bound...就过了

-
P1092. 最短公共超序列
主要练一下带输出答案的dp,题很简单
dp[i][j]代表str1转移到i位,str2转移到j位的最小代价
新开pre数组记录每次dp时候转移的前驱,再倒推输出答案

-
P218 天际线问题
给你若干个矩形,让你描述出最顶端的轮廓
不用stl的话是个线段树染色,涉及到区间染色和单点查询最值,用stl的multiset就能很好的解决这个问题
注意multiset想要删除单个元素需要s.erase(s.find(x)),否则会删除等值的所有元素
那就按照x轴排序,处理完同一坐标的所有内容之后用s.rbegin()获取最大值就好
P1330 翻转子数组得到最大的数组值
稍微有点复杂的一道题
首先显然的,翻转一个区间之后,中间的元素对整体答案的贡献完全不变,那么区别就区别在四个临界元素上:假设反转的区间为[l,r],那么影响答案的四个元素为a,l...r,b,原来的答案为abs(l-a)+abs(b-r),那么变动之后的答案为abs(r-a)+abs(r-b),差值就为abs(r-a)+abs(r-b)-abs(l-a)-abs(b-r)...
是不是晕了?
涉及到绝对值的问题都要尝试拆绝对值,更具体一点就是尽可能分类讨论。因为我们只需要取最大值,那么就可以暴力枚举每种可能然后取个max就好。
循环的思路肯定是固定一侧(即l,a)而枚举另一侧(r,b),那么之前的-abs(l-a)-abs(b-r)就可以扔到一边,我们根据前面的四种情况拆绝对值之后变成四个式子:a-l+b-r
-a+l+b-r
-a+l-b+r
a-l-b+r那么循环的时候a,l的部分是固定的,我们只要维护右侧b,r的后缀max值:
+b-r-abs(b-r)
-b+r-abs(b-r)和左边取max就行。注意到l,r不能为边界,故边界需要再特判一下。
-
P42 接雨水
也是个单调栈的问题,画一下就知道最后形成的形状一定是一个类似于小山的(存在一个最高点,两边递减),那么就先确定最高点的位置(存在多个最高点任意选一个不影响结果),可以用单调栈把左右两侧的轮廓算出来,答案就出来了P2818. 操作使得分最大
很缝合的一道题
每个点的得分可以用线性筛+分解质因数来预处理,单次查询是log级别的。然后我们去计算每个点的总贡献:先预处理每个点向左、向右”延展“的数量,即向左/右中value小于该点的值有多少个,这一部分可以用单调栈优化(怎么又是单调栈= =),设向左延展的长度为l,向右为r,那么该点一共能贡献的区间数量就是(l+1)*(r+1)了。排序之后贪心即可 -
啊???
-
诈尸
P1955. 统计特殊子序列的数目
简单的线性dp, dp[i]代表着取完数列中位置i的数字后的子序列个数
暴力转移n^2,但是因为题目数字只有三种所以合并状态就行了P2528. 最大化城市的最小电量
一般这种带"最小值最大"的题目都是二分答案,答案显然具有单调性,那么这个问题可以转化为能否存在一种分配方法使得总电量均大于k
从左到右贪心就行,尽可能的将供电站靠后建,具体的说就是利用一个滑动窗口来进行维护,当一个数字将要出队列的时候检查它的电量是否达标,实际上就是区间和的问题,同样用滑动窗口维护
边界还是有点恶心的,就是最靠右的几个供电站我第一次忘判了,可以特判也可以暴力的将数组拉长至两倍(右边用0补齐) -
鲸哥有空讲讲ologn求两个有序数组的中位数,我上次和同事没云出来
-
@Starmie
这个模型可以推广为O(logn)求两个有序数组合并之后的第k大问题
第k大,就是把数组里面前(n-k)个比它小的数字都删了,答案就一眼丁真了
简单的想法就是效仿普通的归并,每次比较数组头两个数字,把小的踢出去,一共要踢(n-k)个比较小的数字
那么我们考虑加速,有没有可能同时踢某个数组的一段数字呢?当然是可以的,为了方便起见我们假设剩下还需要踢k个数,那么这两个数组中一定存在某个数组,它的前floor(k/2)个数是可以直接踢出去的
具体的,我们比较这两个数组中的第k/2个数字大小(数组长度不足k/2则取末尾),更小的那个,它以及它之前的数字是一定可以全踢的
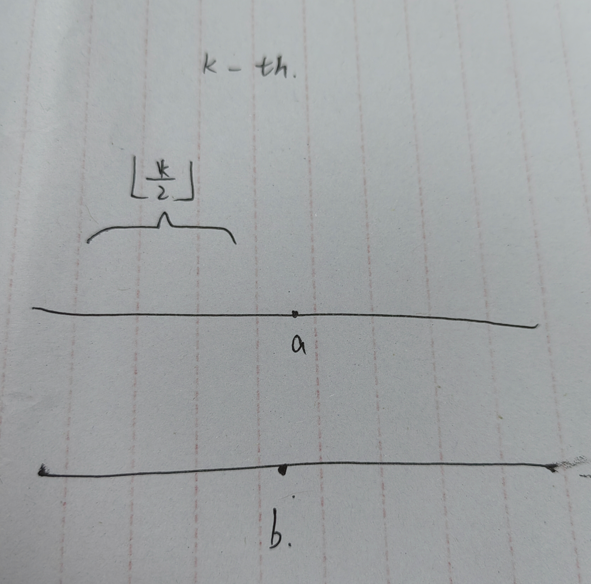
那么原本一共要踢k个数字,每次k值折半,严格logn级别(lc上好像有原题我今天有空了写一下)
edit:
-
面试题 17.20. 连续中值
随机产生数字并传递给一个方法。你能否完成这个方法,在每次产生新值时,寻找当前所有值的中间值(中位数)并保存。
动态维护集合中的中位数,要求复杂度均摊O(logn)
首先这题平衡树肯定可以做,有没有更简单的办法呢?
设某个状态中位数已经求出来了为x,那么对于新加的元素:如果元素>x,则新中位数一定为x的后继;<x,为x的前驱,这点很显然
换言之我们只需要维护当前中位数的后继和前驱就好了,但是这个好像又涉及到平衡树了...
假设我们找到了x的前驱为y,那么我们必须要马上获得y的前驱...好消息是,我们不需要对<x的所有数排序,只需要每次获取最大值就行了,是不是很像堆?
所以我们维护一个大根堆和一个小根堆,大根堆维护<mid的数值,小根堆维护>mid的数值就好了,每次插入数字的时候将其与mid比较,当两个堆差值>2的时候及时平衡(就是把一个堆的顶部移到另外一个堆里就好)。面试题 17.19. 消失的两个数字
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
设缺的两个数字为a b
遍历第一遍可以把a+b找到,a一定<(a+b)/2
遍历第二遍把a找到就行了 -
看不懂,感觉很厉害
-
看的想学计算机
-
778 水位上升的泳池中游泳
二分答案+bfs793 阶乘函数后k个零
首先考虑到2*5=0且5的数量远小于2,不难发现F(x)实际上就是从1到x的数组中所有5的因数个数(当然我是打表之后强行总结的哈哈)。
那么第一个问题就是快速求F(x),x/5显然是1到x中能被5整除的个数,那么把这个数字再/5就是能被25整除的个数,这样递归一下就行,复杂度O(logN)。
之前的打表发现:凡是存在x,k使得F(x)=k,那么满足上式的x的数量一定为5,换句话说我们只要验证给定的k,是否存在某一个x即可。F函数显然单调,二分一下就行了。
复杂度两个log -
@xujing691691 希望你夺冠以后,不要忘记狠狠奖励自己。
-

k=2的时候就是传统区间dp,那么k>2的时候怎么做呢?
一个简单的思想就是记dp[i][j][k]为区间i-j中还剩k堆石子的最小代价,两个区间要么执行合并操作要么不合并石子单纯合并区间。然后思考之后发现第三维k也是多余的:dp[i][j]代表把i-j里面的所有石子合并到不能再分的最小堆数的最小代价,显然这个最小堆数是个定值。
转移的时候分类讨论两种情况:
1.不合并石子单纯合并两个区间,必须保证合并之后的石子堆数严格小于k
2.全部合并,必须保证合并之前两个区间的堆数总和为k典型的区间DP O(N^3)
想法不算难但是细节很多的一道题
环形区间一般可以通过拉长到两倍长度当线段处理,然后这道题乍一看答案具有很强的单调性,那么简化之后的模型就是【给定一个初始积分x,问是否能填满整个线段】,朴素的暴力是O(N^2)的显然不行。
下一个想法就是初始将所有积分<=x的关卡都看为原点,然后暴力左右扩张合并,直到不能合并为止。合并的顺序也有说法,权值越大的点合并的顺序就尽量要越晚,考虑到区间1遇到一个障碍物p无法与区间2合并,之后p被消除,进行区间合并的时候,区间2显然可以无脑接受区间1中的所有顶点(权值一定<p),而反过来就不行了。
那就把整个环看成一张图做并查集,合并的时候还需要维护区间的左右界,总之细节不少。
那么就二分最终答案...交了最终代码之后发现答案错误,发现这个答案他并不具有单调性!因为或的原因可能存在下面一堆低位1可以通过但是上面一个高位1不能通过,那就把答案初始化赋值为全1,然后从高位到低位尝试删除1之后判断能不能通过,贪心一下就好。
复杂度O(nlogp),实际上logp就是long long的位数。

状压dp,dp[i][j]看作已经完成前i个位置的所有防护的同时,第i+1个位置的防护状态为j,j按照1-5秒压缩状态即可
-

不难发现某一行/一列中的棋子颜色排布只满足两种情况:
1.红/黑纯色
2.红黑一个一个交替爆搜出合法状态之后状压dp,每个位置有七种状态:
0-该位置之前未放置棋子
1/2-该位置之前放置过恰好一个红/黑棋子
3/4-该位置之前放置过多个红/黑棋子
5/6-该位置为红黑交替且最后一个位置恰好为红/黑色
树上按照dfs序一边处理子节点,获得路径之后按照字典序排序在子树树根递归合并
-
这几天要去面试了
-
@xujing691691 好好调整,等你请我吃华莱士
-
@xujing691691 gogogo鲸哥